Wooden railways typically have points that don't switch; you just push the train where you want. So how can a train powered by battery reach everywhere? Designing layouts so that happens is the problem described here.
The basic rule is that the train will go straight ahead if it reaches some points. There is no problem coming in to points from either of the branches - unlike some of the ‘bigger’ railway systems where coming in the wrong branch can cause a derailment. Incidentally many wooden railways do also have points which can be switched - but that’s cheating here. Crossings are fine and useful though I’ve avoided them in the examples below. They can be treated like bridges, or you might like to try just pure points only layouts.
Two types of layout are considered here. Firstly layouts where the train reaches everywhere from everywhere by just going forwards. And secondly ones where one can reverse the engine and reach everywhere that way (the remote control engine I got recently was really for my grandson. This is just a welcome bonus :) Honestly.)
I call layouts where the train goes everywhere pancursal, it’s just a word I made up as I don’t know a better one ;-)
This was inspired by an article Laying Track by Ivars Peterson describing work by Mark R. Snavely, James D. Beaman and Erin J. Beyerstedt on train track layouts.
I'm not going to try and enumerate the various solutions here, just show some layouts. Perhaps I’ll do more later but you might like these initial layouts for now. A few rules that become obvious early on though are:
It isn’t quite so obvious but the inverse of the last can be done - every closed figure that can be drawn without lifting a pencil and has only 4 lines joining at a point can be turned into a working layout - quite often more than one. Each joining point is replaced by two railway points. However it may not be possible to go in the same order as the pencil went.
If you click on these images it should bring up some animated SVG - but unfortunately Internet Explorer does not yet support animated SVG. Practically any other browser will be okay.




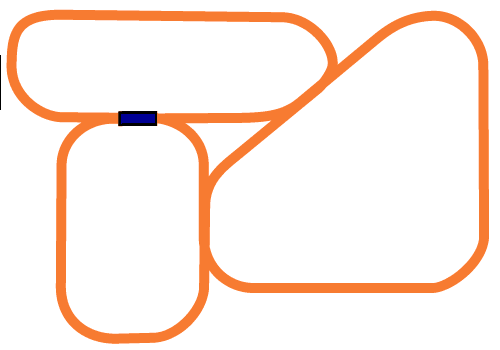

With a remote control engine one can reverse it at any time. This greatly increases the number of circuits where anywhere can be reached from anywhere else.
I’ve restricted myself to points with two outputs here. With a reversing train a three output point is the same as two output points with the second point attached to the straight line output of the first.
Checking a train can reach everywhere if it can reverse is more difficult than for the one way train:
Firstly it doesn’t matter which way a curved track joins a straight track at a point. A point can be considered as a straight line plus a one way entry from the curved track.
Each piece of track is on a 'straight-connected' path where the engine can go back and forth without leaving the path. These straight-connected paths either form circles or have two ends where they join points via the curved paths and so cannot come back the same way.
The simplest case is a single straight-connected path where of course everywhere can be reached from anywhere. This will either form a circle or else have two ends which come back in via two points.
With more than one straight-connected path one can’t have circles otherwise the engine would get stuck on them.
The layout can then be simplified by considering each straight-connected path as a single node, which has two arrows leading away from it to itself or other nodes, and any number of arrows coming in.
A set of nodes connected by arrows is called a directed graph and there are closure algorithms for checking whether everywhere can be reached from everywhere else. In general these algorithms produce a 'directed acyclic graph' where the nodes are groups of the original nodes that can all reach each other, but once they go to another node they can never come back.
And now I have to go off and produce some nice JavaScript to animate trains instead of the SVG I tried - its support is abysmal and gotten worse with the latest version of Microsoft’s Internet Explorer. They obviously hate it and want to kill it.
And a bit of fun - with real engines these two would eventually crash rather than staying in lockstep

This shows two patterns where a crossing is simulated using points. The train goes from one green circle across the layout to the opposite green circle and it does this for both ways and both directions.