A 'wiggly triangle' is a three sided figure whose sides don't have to be straight. They have angles at their corners and a 'right wiggly triangle' is a wiggly triangle whose three corner angles add up to 180 degrees.
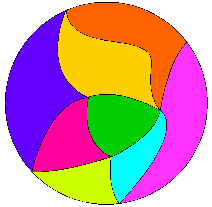
A circle split into wiggly triangles. There are 9 faces - 8 triangles plus the outside, 7 vertices and 14 edges.
The puzzle is in two parts which you should do in order:
First you have to show using the Euler-Descartes formula
faces + vertices = edges + 2
or otherwise that it is impossible to divide a circle into a finite number of right wiggly triangles.
Your friends take you to a bunco booth, where the carnie says he can divide up a circle as described above. Will you put your money where your mouth is and bet against him, if only to see what he has done. Or can you do the impossible? :)
There are Solutions here but have a go first.